Алгоритмы компьютерной графики

2.1. Математическое описание векторной графики
2.1.1. Кривые Безье
Одним из основных элементов векторной графики являются кривые Безье. Метод кривых Безье позволяет создавать кривые любой формы. Они широко используются для решения задач аппроксимации, так как их удобно описывать аналитически и они просты для наглядного геометрического построения. Независимо друг от друга кривые Безье были разработаны двумя инженерами из французских автомобильных компаний Полем де Кастелье ("Ситроен") и Пьером Безье ("Рено") для проектирования кузовов автомобилей. Несмотря на то, что де Кастелье изобрел их раньше(1959 год), первым достижение представил публике Пьер Безье в 1962 году.
Впоследствии кривые Безье стали широко использоваться не только в автомобилестроении, но и в системах автоматизированного проектирования и программах компьютерной графики для модерлирования гладких линий; однако не все виды кривых Безье имеют широкое применение в компьютерной графике - кривые высших степеней используют редко ввиду их высоких требований к вычислительным ресурсам, поэтому наиболее популярными являются кубические кривые Безье (для создания сложных линий, кривые объединяют в сплайны).
Кривая Безье задается многоугольником и имеет математическое параметрическое представление вида:

где базис Безье или Бернштейна, или функция аппроксимации


 -  это i-тая функция базиса Бернштейна порядка n. Здесь i — порядковый номер опорной вершины, n — порядок определяющей функции базиса Бернштейна — и, следовательно, сегмента полиномиальной кривой, на единицу меньше количества точек определяющего многоугольника.

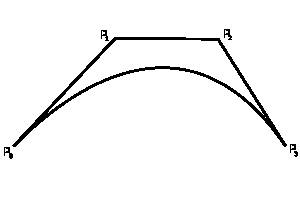
Рис. 2.1. Кривая Безье и, образующий ее, многоугольник

 - биномиальные коэффициенты.
 - функция компонент векторов опорных вершин (координаты вершин многоугольника Безье).
Метод de Casteljau основан на разбиении отрезков, соединяющих исходные точки в отношении t (значение параметра), а затем в рекурсивном повторении этого процесса для полученных отрезков.
Кривые Безье бывают линейные, квадратичные, кубические и т.д. - кривые высших степеней. Линейная кривая Безье является отрезком и задается двумя опорными точками, которые являются концами этого отрезка; квадратичная кривая имеет 3 опорные точки; далее аналогично.
Примеры математического писания сплайнов 1,2,3-его порядков:


  
Преобразование квадратичных кривых Безье в кубические:
Квадратичная кривая Безье с координатами  преобразовывается в кубическую кривую Безье с координатами 
Некоторые свойства кривых Безье:

• Функции базиса вещественны.

• Степень многочлена, определяющего участок кривой, на единицу меньше количества точек соответствующего многоугольника.

• Основа формы кривой повторяет очертания многоугольника.

• Первая и последняя точки кривой совпадают с соответствующими точками определяющего многоугольника.

• Векторы касательных в концах кривой по направлению совпадают с первой и последней сторонами многоугольника.

• Кривая лежит внутри выпуклой оболочки многоугольника, т.е. внутри самого большого многоугольника, построенного по заданным точкам.

• Кривая обладает свойством уменьшения вариации. Это означает, что кривая пересекает любую прямую линию не чаще, чем определяющий многоугольник.

• В случае, если выпуклые оболочки не пересекаются, то и сами кривые не пересекаются.

• Кривая инвариантна относительно аффинных преобразований.

2.1.2. Сплайны
Изначально сплайны использовались при проектировании технических объектов в системах автоматизированного проектирования (САПР), позднее их стали использовать в программах двух- и трехмерной графики.
Сплайн (от англ. spline) — полоска стали, с помощью которой проводятся плавные кривые через заданные точки.

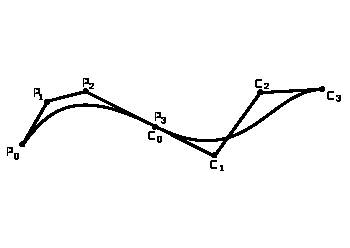
Рис. 2.2. Сплайн, составленный из двух кривых Безье

Сперва сплайны использовали, как удобный инструмент в теории и практике приближенных функций, впоследствии область их применения расширилась. Теперь сплайны используются в численных методах, в системах автоматического проектирования и автоматизации научных исследований, а также для создания изображений в компьютерной графике.
Для большинства тел, встречающихся на практике, не существует простых универсальных формул, описывающих соответствующие контуры объекта в целом. Поэтому при изображении произвольного объекта, как правило, не удается обойтись небольшим количеством простейших формул, и тогда на помощь приходят сплайны. Обычно при создании изображения сначала задают координаты небольшого числа опорных точек, описывающих будущую кривую линию или контур, а затем эти точки объединяют плавной кривой.
Сплайны применяются для решения двух следующих задач: по заданному массиву опорных точек на плоскости необходимо построить кривую, проходящую либо через все эти точки - задача интерполяции, либо вблизи этих точек — задача сглаживания. Для решения этих задач используются различные методы, например задачу интерполяции используют многочлен Лагранжа. К его достоинствам относят простоту описания и точность прохождения через вес точки, к недостаткам то, что степень многочлена Лагранжа лишь на единицу меньше числа заданных точек, также изменение координат одной точки требует полного пересчета коэффициентов интерполяционного многочлена и существенно влияет на вид задаваемой им кривой. Интерполяционную кривую можно построить с помощью ку­сочно-линейной интерполяции, т.е. путем последовательного соединения точек заданного набора отрезками прямых, результате будет ломаная линия, но полученная таким образом кусочно-линейная функция не обладает нужной гладкостью и не может быть использована для создания контуров объектов даже при большом наборе опорных точек. Для оптимального решения задачи интерполяции необходимо использовать так называемый полиномиальный многозвенник, который сочетает преимущества двух рассмотренных выше способов: для интерполяции используются многочлены фиксированной сте­пени, интерполяция производится последовательно — звено за звеном. При этом важно правильно выбрать степени интерполя­ционных многочленов, а также коэффициенты многочленов для выполнения условия гладкого сопряжения соседних узлов. Полученные в результате интерполяции функции называются сплайн-функциями или просто сплайнами.
В случае с векторной графикой, чаще всего приходится решать задачу плавного соединения кубических кривых Безье, условия для состыковки кривых Безье в сплайн.

2.1.3. Алгоритмы заливки плоских фигур
Основными примитивами векторной графики являются линия и образованный с ее помощью контур (открытый или замкнутый). Параметры обводки контура определяют его вид при отображении. К ним относятся:

• толщина линии обводки;

• цвет линии;

• тип линии (сплошная, пунктирная и пр.);

• форма концов (со стрелкой, закругленные и пр.).

Замкнутые контуры обладают особым свойством — заливкой, т.е. параметрами заполнения охватываемой контуром области.
Существует несколько типов заливок:

• заливка основным цветом, т.е. заполнение внутренней области выбранным цветом;

• текстурная заливка - заполнение узором с регулярной структурой;

• заливка изображением-картой (узором) - заполнение готовым растровым изображением, называемым картой;

• градиентная заливка - заполнение двумя цветами с плавным переходом между ними.

Для каждого вида заливок существуют свои алгоритмы.
Заливка основным цветом
Первоначально необходимо определить область заливки. Существует несколько способов задания областей, ограниченных контурами:

• Внутренне-определенные области: существуют группы точек находящиеся снаружи и внутри контура, имеющих различные значения кода цвета или яркости внутри и вне данного контура.

• Гранично-определенные области: существуют некоторые «затравочные» точки, в соответствии со свойствами которых производится закраска всей области.

• Области, заданные списком вершин, например для закраски гранично-определенных областей существует несколько алгоритмов, к примеру рекурсивный метод.

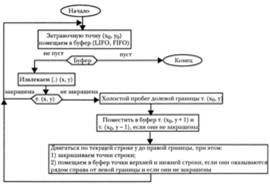
Рис. 2.3. Рекурсивный алгоритм заливки

Рекурсивный метод прост для программирования, однако считается низкоэффективным. От затравочной точки просматривают все точки. Если они не граничные, их закрашивают и код соответствующего цвета записывают в стековую память. Далее производится считывание данных из стека, и если очередная точка не является граничной и закрашенной, ей присваивают тот же код.

Текстурная заливка
Текстурные заливки — это такие заливки, в которых все внутреннее пространство объекта заполняется единым рисунком, отображающим текстуру таких поверхностей, как металл, облака, дерево, цемент и т.д., с помощью специально созданных цветных растровых изображений. Арсенал текстурных заливок представляет собой обширный набор таких математических моделей, у каждой из которых имеется уникальный набор управляющих параметров. Эти модели распределены по нескольким библиотекам, в которых хранятся несколько десятков описаний текстур и у каждой есть имя, описывающее ее внешний вид. Основным параметром каждой из моделей, по которым строится изображение, является номер текстуры.

Заливка изображением-узором (картой)
Узоры представляют собой заливки в виде набора заранее подготовленных однотипных прямоугольных ячеек заполненных оригинальным рисунком. В результате использования такой заливки внутреннее пространство объекта заполняется совокупностью этих ячеек, что образует непрерывный рисунок. Простейший вариант заливки узором — это двухцветный узор, например черно-белый. Полноцветный узор (векторная заливка) — это полноцветный узор с использованием и линий, и заливок. С помощью узорных заливок можно создавать мозаичные фоны или повышать реалистичность создаваемых изображений (при использовании растровых заливок). Все заливки состоят из небольших квадратных плиток, которые складываются в правильную мозаику без искажений. Очень важно, что данный тип заливки позволяет в интерактивном режиме изменять элементарные части, что позволяет создавать новый, совершенно не похожий на исходный, узор.

Градиентная заливка
Градиентом называется постепенный переход от одного оттенка или цвета к другому оттенку или цвету. Градиентные заливки в отличие от однородных отображают сложные цветовые переходы между различными цветами. Добавляя в градиент необходимое число промежуточных цветов, можно формировать многоцветные градиентные заливки. В этом случае градиентную заливку можно трактовать как своеобразный узор, образуемый постепенным переходом между двумя или несколькими цветами или оттенками одного итого же цвета. В зависимости от направления перехода цветов существует четыре типа градиентных заливок: линейная, радиальная, коническая и квадратная. Цветовая гамма градиента определяется серией опорных точек, которые обозначаются на шкале цветового перехода специальными маркерами: начальный маркер, конечный маркер цвета и промежуточные маркеры. Опорными точками применительно к градиенту называют точки, в которых тот или иной цвет присутствует в количестве 100% и не смешивается с другими цветами. Маркеры опорных точек можно сдвигать относительно друг друга, настраивая тем самым цветовой рисунок градиента.

2.1.4. Визуализация кривых Безье и шрифтов
При расчете и последующей визуализации кривых Безье в основном используются два метода: прямой метод и метод разбиения (subdivision).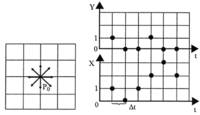
Рис. 2.4. Прямой метод

Построение кривых Безье прямым методом:
x=x(t),
у=y(t),

Подберем шаг dt так, чтобы dx и dy были меньше 1 (т.е. мы не пропустим ни одного пиксела).    и  многочлены, поэтому легко найти их максимумы Мх и Му. Положим M = max(Mx,My). Тогда, взяв , получим, что смещения по х и по у при каждом шаге не превосходят 1. Недостатком этого метода является то, что при малых смещениях по х и у много итераций рассчитывается впустую.

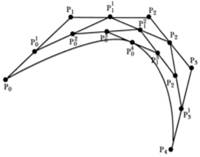
Рис. 2.5. Метод разбиения

Построение кривых Безье методом разбиения:
Если рассмотреть участок между P0 и  , взятых для t=0,5, то он может быть задан как кривая Безье с опорными точками . Аналогичные рассуждения справедливы и для участка между   и P4. Таким образом, можно применить этот алгоритм рекурсивно для левой и правой частей, пока размер участка кривой не станет меньше размера пиксела.

Исходя из того, что векторный шрифт - это шрифт, основанный на представлении символов (алфавита) в виде множества кривых, способы его визуализации идентичны способам визуализации кривых. Так, например, в TrueType для описания формы символов используются сплайны, составленные из квадратичных кривых Безье.